Mathematics For Machine Learning(part-II)

 Continuee.... 

Statistics

population: A collection or set of individuals or events  or objects whose properties are need to analyze

sample: A subset of population is called 'sample'. A good sample contais all the information realed to the population

Sampling is divided into two groups:

1.probability       2.non-probability

probability:

Random sampling: every member of the population has an equal chance of being selected. This can be achieved by using random number generators or drawing names out of a hat, for example.

Systematic sampling:Systematic sampling involves selecting members from a larger population at a regular interval, or "kth" number. The starting point is chosen randomly, and then every kth member is selected until the desired sample size is reached.

Stratified sampling:Stratified sampling divides the population into smaller groups, or strata, based on shared characteristics. A random sample is then taken from each stratum. This method ensures representation of all significant subgroups within the population

Types of statistics

Descriptive statistics

Descriptive statistics aim to describe and summarize the main features of a dataset. They provide simple summaries about the sample and the measures. These summaries can be either quantitative (numerical) or visual.

Measures of Central Tendency: These include the mean (average), median (the middle value when data are ordered), and mode (the most frequent value).

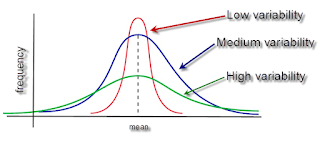
Measures of Variability (Spread): These include range (difference between the highest and lowest values), variance (average of the squared differences from the Mean), standard deviation (square root of the variance), and interquartile range (difference between the 75th and 25th percentiles).

Inferential statistics

Inferential statistics use a random sample of data taken from a population to describe and make inferences about the population. Inferential statistics are valuable when it is not convenient or possible to examine each member of an entire population. They are used to estimate population parameters, test hypotheses, and make predictions

Entropy

Definition: A measure of the uncertainty, randomness, or disorder in a dataset.

Context: Widely used in information theory to quantify information content and in machine learning for assessing homogeneity in datasets.

formula:-p * log2(p) - (1-p) * log2(1-p), where 'p' represents the proportion of one class in the dataset

Interpretation: Higher entropy indicates more disorder or uncertainty in the data, while lower entropy indicates more order or predictability.

Information Gain

Definition: The reduction in entropy or uncertainty about a dataset resulting from dividing it on an attribute.

Context: Key in decision tree algorithms for selecting the attribute that best splits the dataset, aiming to form subsets with higher homogeneity.

formula:

IG(D,A)=H(D)−H(D∣A), 

where H(D) is the entropy of the whole dataset and H(D/A) is the weighted sum of the entropy for each subset after splitting on attribute 

Interpretation:

 Information gain quantifies the effectiveness of an attribute in reducing uncertainty. 

Attributes that result in high information gain are preferred for splitting the dataset in decision tree models.

Confusion Matrix

A confusion matrix is a specific table layout used in machine learning and statistics to visualize the performance of an algorithm, usually a classification model. It is a powerful tool for summarizing the accuracy of a classification model in a concise manner. The matrix compares the actual target values with those predicted by the model, allowing the identification of errors and the overall effectiveness of the model.

True Positive (TP): The model correctly predicted the positive class.

True Negative (TN): The model correctly predicted the negative class.

False Positive (FP): The model incorrectly predicted the positive class (also known as a Type I error).

False Negative (FN): The model incorrectly predicted the negative class (also known as a Type II error).

Point Estimation

Definition: Point estimation involves using the data from a sample to compute a single value (known as a point estimate) that serves as the best estimate of an unknown population parameter (e.g., population mean, μ, or population proportion, p).

Example: If you measure the heights of 50 people and calculate the average height to be 170 cm, that value (170 cm) is a point estimate of the average height of the entire population from which your sample was drawn.

Interval Estimation

Definition: Interval estimation, on the other hand, uses sample data to calculate an interval of possible values within which the true population parameter is expected to fall. This interval is known as a confidence interval (CI) and is associated with a confidence level (e.g., 95% confidence level) that quantifies the degree of certainty (or confidence) in the interval estimate.

Example: Continuing the example above, instead of stating the average height as a single point estimate (170 cm), you might calculate a 95% confidence interval of 165 cm to 175 cm. This means you are 95% confident that the true average height of the population falls within this interval.

Probability

A random experiment

Random experiment is a fundamental concept in probability theory, referring to a process or procedure that generates a well-defined set of possible outcomes. The key characteristics of a random experiment are that it can be repeated under the same conditions, and the outcome cannot be predicted with certainty beforehand, although the set of all possible outcomes is known

sample space

The sample space in probability theory is a fundamental concept that represents the set of all possible outcomes of a random experiment. It is denoted by the symbol S or (omega) .and each outcome within the sample space is known as a sample point. 

Event

In probability theory, an event is any collection of outcomes from a random experiment's sample space. It represents a subset of the sample space that satisfies some condition or set of conditions.

Joint Events

Joint events refer to events that can occur together; that is, they have at least one outcome in common. The concept of joint events is closely related to the intersection of sets in set theory.

Disjoint Events (Mutually Exclusive Events)

Disjoint events, also known as mutually exclusive events, are events that cannot occur simultaneously. In other words, if two events are disjoint, the occurrence of one event precludes the occurrence of the other.

Probability Density Function 

A Probability Density Function (PDF) is a fundamental concept in statistics and probability theory, particularly when dealing with continuous random variables. The PDF helps describe the likelihood of a continuous random variable taking on a specific value.

 Unlike discrete random variables, which have probabilities assigned to individual outcomes, a continuous random variable has an infinite number of possible values, and the probability of it taking on any single exact value is essentially zero. 

Instead, the PDF provides the density of probabilities across a range of values, allowing us to calculate the probability of the variable falling within a specific interval.

The Central Limit Theorem (CLT)

The Central Limit Theorem (CLT) is a fundamental principle in statistics that describes the distribution of sample means. 

It states that, under certain conditions, the distribution of the sum (or average) of a large number of independent, identically distributed (i.i.d.) random variables, regardless of the original distribution of these variables, will approximate a normal distribution. 

This convergence towards normality occurs as the sample size becomes sufficiently large.

Joint probability

Joint probability refers to the likelihood of two or more events happening together. It's like asking, "what's the chance of both event A and event B occurring?

Conditional probability

Conditional probability refers to the likelihood of event B happening given that event A has already occurred.

Imagine you have a bag with 3 red marbles and 2 blue marbles. You randomly draw one marble:

Event A: Drawing a red marble (P(A) = 3/5)

Event B: Drawing a blue marble (P(B) = 2/5)

Initially: There are 2 blue marbles out of 5 total (P(B) = 2/5).

After drawing a red marble: We remove it, leaving 4 marbles.

Now: There are only 2 blue marbles left out of 4 (P(B|A) = 2/4).

Therefore, the probability of drawing a blue marble after drawing a red marble is 2/4, or 1/2, 

which is higher than the initial probability of 2/5. This shows how knowing one event happened (drawing a red marble) affects the probability of another event (drawing a blue marble).

Baye's Theorem

Bayes' theorem helps us update our beliefs about something (event A) after observing new evidence (event B). It tells us how the probability of event A changes considering the knowledge of event B.

P(A1): You know 80% of your patients with coughs have the common cold. (P(A1) = 0.8)

P(A2): The remaining 20% have pneumonia. (P(A2) = 0.2)

P(B|A1): You also know that 90% of patients with the common cold have a cough. (P(B|A1) = 0.9)

P(B|A2): However, for pneumonia, only 50% of patients have a cough. (P(B|A2) = 0.5)

Question: Given the patient has a cough (event B), what is the updated probability they have the common cold (event A1)?

Bayes' Theorem:

P(A1|B) = [P(B|A1) * P(A1)] / [Σ [P(B|Ai) * P(Ai)] for all possible Ai]

Applying the formula:

P(A1|B) = (0.9 * 0.8) / [(0.9 * 0.8) + (0.5 * 0.2)] = 0.643 / 0.74 = 0.87

Interpretation:

Even though the common cold was initially more likely, after considering the cough symptom, the probability the patient has the common cold increases to 87%. 

This shows how Bayes' theorem updates our beliefs based on new evidence.